Optimus Prime

Find out all prime nos upto N - Sieve of Eratosthenes

Hola! Don’t get swayed by the Greek name.

I don’t think I need to explain what prime nos are. Finding prime numbers if tough, because they don’t follow a pattern, like even or odd numbers do.

Essentially, the only way you can tell if a number is prime to check its factors and see if one and the number itself are the only ones. And that’s not something that you can optimize.

Think about that for a minute. You can’t optimize the procedure of checking, but you CAN optimize the number of numbers you have to check, can’t you? For instance, there’s no point checking any multiples of 2, because we know that they’re gonna have 2 as a factor other than 1 and the number itself, and are therefore, not prime.

Similarly, there’s no point checking any multiples of 3, same reason. So, for all prime numbers we find, if we flag all their multiples as not prime, we can cut down the numbers we have to check, correct?

Spot on! And that’s what SoE does.

And there’s another optimization that you can do.

For a number n, there’s at max, only one prime factor > sqrt(N).

There’s a proof involved, but we’ll leave that for another post. Just think about it,

39 has factors 1,3,13,39. 13 is the only factor > sqrt(39)~6.3. And 13 is multiplied by 3 to get 39. 3 < sqrt(39). That means, that we only need to check for factors till sqrt(N).

So, finally, all that we have to do is, start at 2, mark all the multiples of 2 not prime, go to the next non-prime, that is 3, follow the same, until sqrt(N). Finally, we return all the primes.

Here’s an implementation :

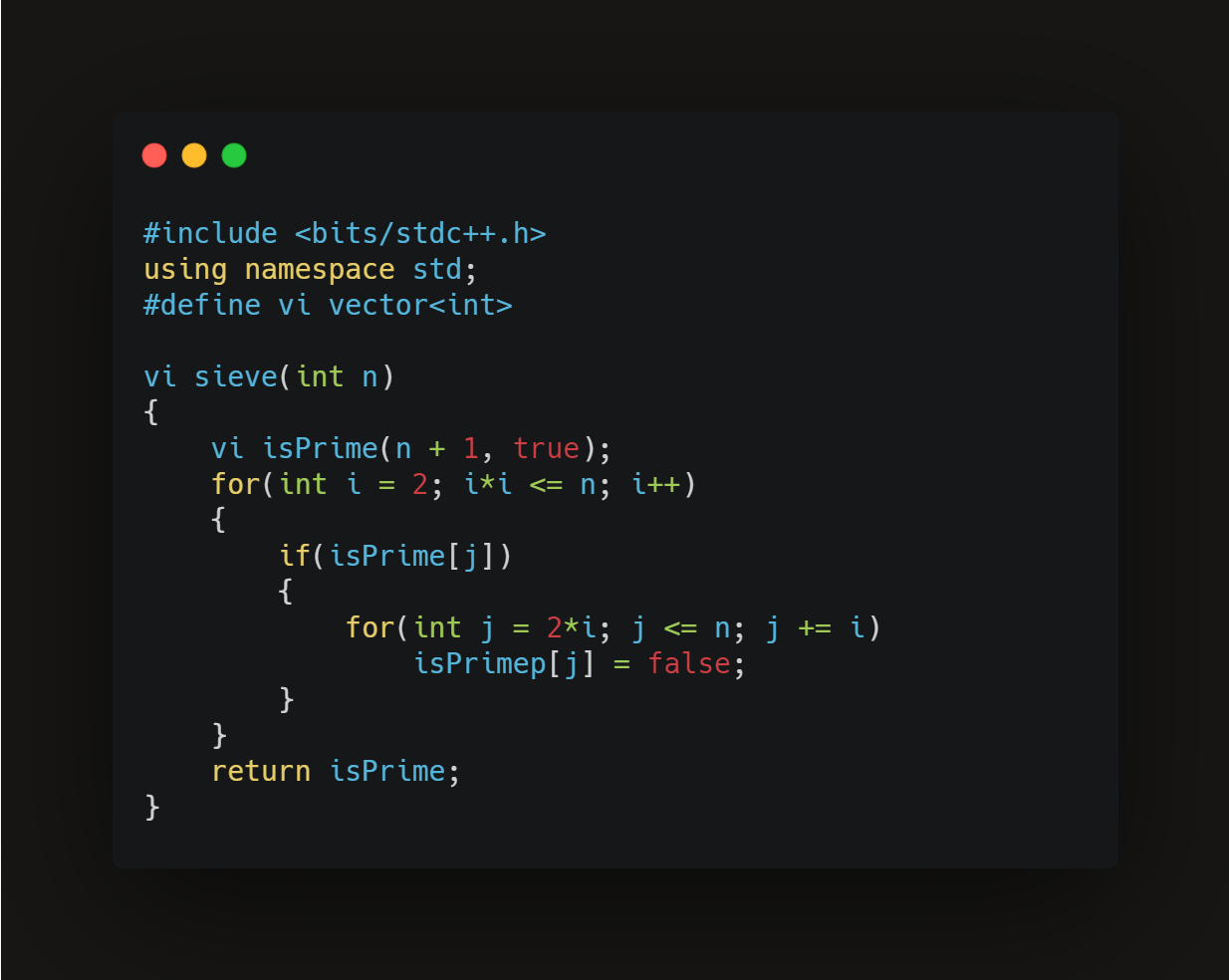
Time complexity : For every i, the code inside the first for loop runs different number of times, so, we won’t consider the outer for loop, but take each of the inner runnings separately.

When i is NOT PRIME, it’s a constant time, so that’s out. When is prime,

Total time for inner = N/2 + N/3 + N/5 + ……..= N(1/2 + 1/3 + 1/5 + …….)

Again, the proof of this series is too lousy to include here, here’s a link if you’re adamant on looking into it. I’ll just say it comes out to be O(log(log(N))).

Therefore, the final TC is O(N*log(log(N))).

Space complexity is O(N), our resulting vector.

From the time complexity, you can see that this logic would work for N~10^7. What if it’s more? There’s another way, but with some preconditions. That’s for the next post.

See ya!