Merge Sort

A common sorting algo; how it works, why is it better?!

If I was asked to pick one question, that is CLAIMED to be fiendishly simple, basic, and yet, a personal favorite of interviewers, it'd have to be merge sort. Not just because I was asked this very question across 3 different interviews, out of which I could answer well enough in only the last one, it is considered to be a test of your intuition. 

Merge sort is based on Divide and Conquer strategy, meaning you break a big thing down into many smaller things, and solve them one by one. Think about your life. When your life's messed up, you don't go about trying to set it right all at once. 

You do it, ONE THING AT A TIME. Life lesson, yes, coding lesson, yes too. And that's what merge sort does. Instead of trying to sort the entire array in one go, it breaks it down, and tries to solve the parts. 

It's important performance-wise, because we perform it in O(N) time, as opposed to other sorting algorithms that take O(N^2) time.

So, how does it work?

Algorithm : - 

• Keep breaking the array in half, until there's only single elements left

• Join two single elements in sorted fashion. So, for four elements, you get two sets of two elements, both of which are sorted individually, but might not be sorted on the whole. 

• Now, we merge the two, two element arrays in a sorted fashion, to get one array, that's also sorted.

• Finally, repeat this procedure until we get the whole array back.

  
  For instance, 6 3 7 1 -> 6 3 | 7 1 -> 6 | 3 | 7 | 1 -> 3 | 6 | 1 | 7 -> 3 6 | 1 7 -> 1 3 6 7

  
  Implementation ?
  

  

  You have to keep doing the same thing, until you reach a base case. 
  How? 
  .
  .
  Get a deja vu? 

  
  Ye-xactly!

Recursion!

You have to recursively break down your array into half, until you're left with single elements.
 
And then? We have to merge the smaller pieces in a sorted manner. 

To break pieces, what'd need to pass is the array, with the start and end positions.

A great Software Engineer called DKP once said

If an algorithm looks easy, you haven’t implemented it yet

All we've to do first, is recursively break the array. Now, it's space-wise infeasible to ACTUALLY MAKE TWO SMALLER ARRAYS from a bigger one. So, we break it virtually. (Everything these days seems to be going virtual :P)

We pass in the entire array, but ALONG WITH IT, we pass in the end-points of the two smaller arrays that we want. And what would the end points be? 

Remember we're just halving the array?

So, it's just [start, mid] and [mid + 1, end], where mid = (start + end)/2. 

Doesn't take a scientist to figure that out.

Question 1 : What will we start with? Again, simple, start = 0, and end = size of array - 1, that is, the entire array.

Question 2 : The base case? That is, the condition when the recursion should stop? 

Hint : Think about the end condition for Binary search. 


Right. At a time, start >= end, that is, your array is broken down so much so, that any further breaking down, will give you an array of size 0. Not happening, that. 

So, we return.

Let's see what all of this looks like in the language of the gods.


All that claptrap, and all it gives is these....these....4 lines ?! 

That's the world of software, my friend.

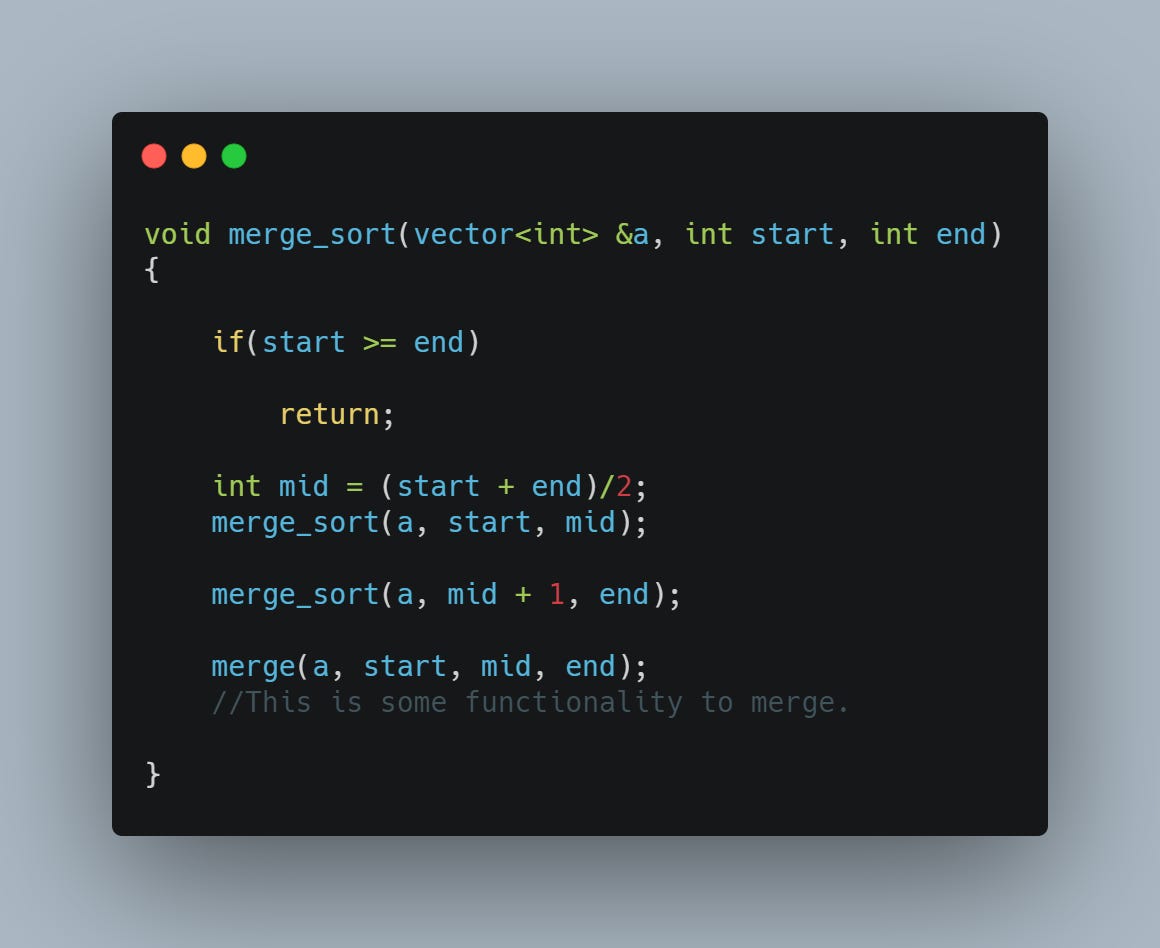
We're far from done yet. We have, so far, managed to break down the array. Now, we need to write functionality for a sorted merge, meaning, given two 'virtual' arrays, make a new 'virtual' array, that will have elements of both the smaller arrays, SORTED.

So, how do we do this? First, we're passing arrays 'virtually', which means that there's only gonna be one array. But, for a sorted merge, we're gonna have to modify that array, so, we need to ACTUALLY CREATE the two separate arrays now, which will be merged into our original array.

Then, we traverse through the two smaller arrays, do an element by element 

comparison. 

The smaller of the two, will be added to our original array.

So, finally, we’ve managed to implement the merge sort.

Time complexity?

Breaking the array into half everytime, takes log(N) time. To convince yourself, consider an array of size 8. Dividing it into half gives us two arrays of size 4. Further halving gives us 4 of size 2. One final halving gives us 8 of size 1. So, we halved it THRICE.

3 = log_2(8) = log(N)

Now, think about the merge operation. We’re traversing through the array of size (end-start) for EACH OF THE LOG(N) levels.

O(end-start) = O(N). Therefore, total time complexity is

O(N*log(N)) = O(N log(N))

Finally, an intuitive confusion : Given that we’re just comparing the elements one by one in the merge function, how is it different from other sorting algorithms? The answer is, the number of swaps.

You’re right, we’re comparing. But, we’re NOT comparing each element with every other element. Rather, once we have two SORTED halves, we’re ONLY COMPARING elements between the halves. Not the elements inside one half.

If you are still confused, try taking an example and work out the number of swaps that merge sort does, as compared to another sorting algo like Bubble sort, and you’ll see the difference.

Space complexity? Well, lemme not just say this right out. Try working it out. Will let out the answer in the next release.

This post can also be found on my blog here, and it would look a lot more beautiful. So, do check it out for a more good looking version.

Hope you found this post intuitive. In case you found some issues reading it as a mail, especially the code, do reach out to me on dushyant@dkprobes.tech and let me know, so that I can take care of it in the next release.

Also, please do share this with any of your friends who might benefit from this, through the button below

Until the next time…

DKP