Binary searching the answer

DSA people's version of hit and trial

Aug 18, 2020

Hola guys

Not gonna say anything as cliche as, “Did you miss me!!“ coz I know you have better things to do.

Anyway, today we’re talking about a concept called ‘Binary searching the answer‘

I just can't excuse the pun here.

Remember how we students are mocked if we don't know the correct method to solve the question, and instead, just try and place values and see if any of it makes the match?

It turns out, if you do the SAME thing, in an optimal way in DSA, not only are you NOT mocked for having just hit-and-trial-ed the answer, but you ALSO get a cool name for the method : Binary searching the answer. And the best part, it's sometimes more optimal than the actual long drawn method.

Binary search be like :

Hope you’re familiar with binary searchIf not, here's a quick crash course :

Suppose you have to find an element inside a sorted array. One thing you could do is traverse through the entire array, looking for the element. It'd be an O(N) solution. Now, can it be made better? Yes, it can, or I wouldn't be writing this.
We know it's a sorted array. So, we know that all given elements to the LEFT of a given element x are going to be smaller than or equal to x, and those to the right, are greater than or equal to x. So, if we're looking for 5, instead of starting from the first element of the array, we hit the middle of the array. If it's a 3, we know we only have to look for 5 in the right half now, that is the elements after 3, because we know that the elements before will all be less than 3. Now, in the right subarray, we again hit the middle of the subarray, and repeat the procedure.
Effectively, in every iteration, we are just kicking out half of the array we have to search, that is, only half the searches we'd have otherwise. This reduces the time complexity to O(log N). Sweet, no?

Feel free to gift me the Presidential Medal of Valor for having explained you binary search in 2 mins.

Now that you're clear on what Binary search is, let's talk about our problem at hand.

Given a SORTED array, containing only 0s and 1s, we have to find the transition point. The transition point is the first ‘1’ in the array.

Now, as you thought, a naive solution would be to keep going until you find a 1, at which point you return the index.

That's O(N), as we saw above. Not good enough. So?

Binary search.

We try binary searching the first one. Don't worry if it sounds strange : We are binary searching, not for ‘a’ 1, but for the FIRST 1 from the left. So, the catch here is,

How the hell do you know if the 1 you have is the FIRST 1?

A 1, is the first 1, if the element right before it, is a 0.

So, how do we go about it? We have a low, the first element, and a high, the last.

Start at the middle. If the middle is a 1, and the element before it is a 0, we have our answer. If not, we have two cases : If the middle is a 0, we have to go to the elements on the right, and if it's a 1, we go to the left. So, for the 0, we set low = mid + 1, that is, ignoring the first half, and if it's a 1 without a 0 before, we set high = mid - 1, ignoring the second half.

We keep going till high is high and low is low.

Sorry. We keep going till low < high. Makes sense, no?

This is what it looks like in code.

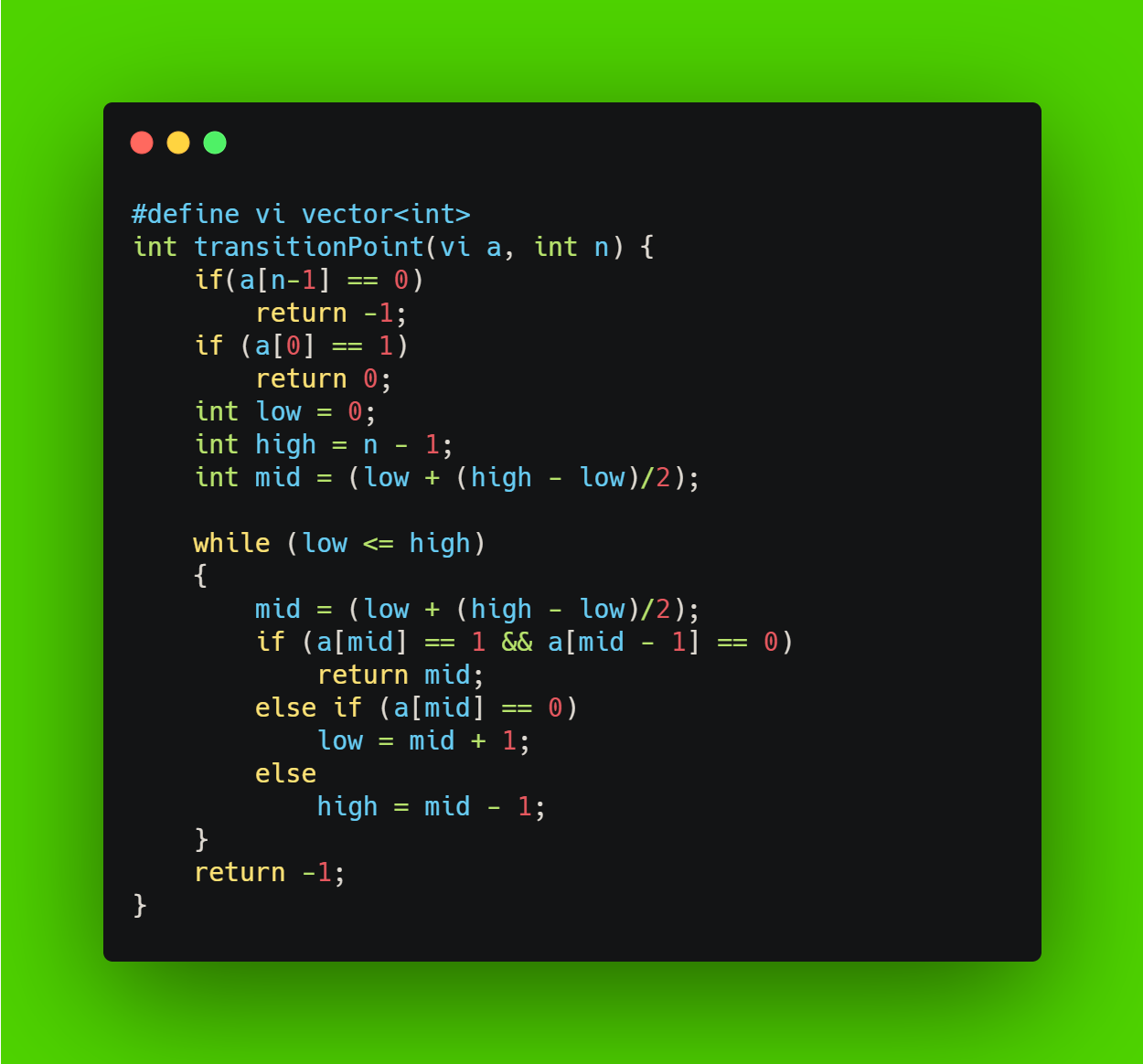
Time complexity? For the first iteration, low is 0 and high is the last element. That's n elements, we need to sift through, worst case. For the second, it's half, aka n/2. For the next, it's halved once again, that's n/4.The total?n + n/2 + n/4 + ... = log_2(n) (log n base 2)

That's it! Here's our (log N) solution, through the much celebrated binary search method.

Binary searching the answer is a method commonly applied across a variety of problems, just like the one above. For instance, looking for the square root of a number without using library square root functions. Try working that one out on your own.

As always, the post is available on my blog here. Also, an addition this time : Complete codes for all posts will be on this GitHub repo. Please do star the repo and follow me for updates.

dkprobescode

Discussion about this post